你知道吗?在数学的世界里,有一种神奇的操作叫做“模2加”。听起来是不是有点儿像魔法呢?别急,让我带你一探究竟,看看这个“模2加”到底是个啥玩意儿,又是怎么在数学的舞台上大放异彩的。
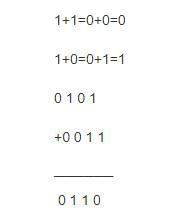
想象你有一个数字,比如说3。现在,我们要用模2加的方式来处理它。模2加,顾名思义,就是用2来“模”这个数字。简单来说,就是将这个数字除以2,然后取余数。所以,3除以2的余数是1。这样一来,3模2加的结果就是1。
是不是有点儿绕?别急,我来举个例子。假设你手里有3个苹果,现在要分给2个人,每个人能分到几个苹果呢?用模2加来算,3除以2的余数是1,所以每个人能分到1个苹果,还剩下1个苹果。

别看模2加听起来简单,它可是在数学和计算机科学中有着广泛的应用呢!
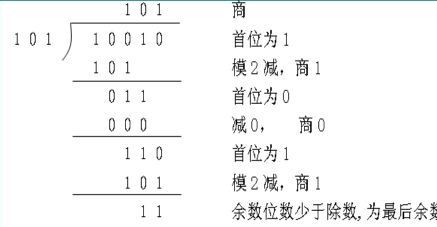
在计算机科学中,模2加有着非常重要的作用。比如,二进制加法就是基于模2加的原理。在二进制中,只有0和1两个数字,所以加法运算就变得很简单了。当你用二进制加法计算两个数时,如果相加的结果大于1,就需要进位。而这个进位的过程,其实就是模2加。
在数学中,模2加也有着它的用武之地。比如,在群论中,模2加就是一个非常重要的运算。群论是数学的一个分支,研究的是具有某种运算的集合。在模2加的群中,所有的元素都是整数,而运算就是模2加。
你可能觉得,模2加不过就是一个简单的运算,有什么神奇的呢?其实,它的神奇之处就在于它的周期性。
你知道吗?在模2加中,任何数字加上它自己,结果都是0。比如,1模2加1等于0,2模2加2等于0,以此类推。这就是模2加的周期性。
这个周期性在计算机科学中有着广泛的应用。比如,在计算机的内存管理中,就需要用到模2加的周期性来保证数据的正确性。
虽然模2加有着广泛的应用,但它在实际操作中也存在一些挑战。
在处理大数时,模2加的计算复杂度会变得很高。这就需要我们寻找更高效的算法来解决这个问题。
在计算机科学中,由于计算机的存储限制,我们无法直接进行无限精度的计算。这就需要在模2加的过程中,处理好精度问题。
模2加,这个看似简单的数学运算,却在数学和计算机科学中扮演着重要的角色。它不仅有着广泛的应用,还蕴含着丰富的数学原理。让我们一起探索这个神奇的数学世界,发现更多有趣的知识吧!